diagrama de flujo de mayor edad hecho por if

calcular la suma de números pares desechando los impares

tutorial de c++ (while, do while , for )

DIAGRAMA DE FLUJO HECHO POR.if_while_for

DIAGRAMA DE FLUJO :WHILE_ Y_ FOR

diagrama de flujo combinados :WHILE_Y _DO WHILE

metodo de ordenamiento por burbuja con ejemplo

Diagrama de flujo de ordenamiento por burbuja

Programación de burbuja en c++


#include<iostream.h>
#include<conio.h>
void main()
{int j,i,n,aux,v[50],k=1,p,x;
cout<<"ingrese numero de vectores:";
cin>>n;
for(i=1;i<=n;i++)
{cout<<"ingrse vector["<<(i)<<"]:";
cin>>v[i];
}
{for(p=1;p<3;p++)

for(i=1;i<=n-1;i++)
{
for(j=1;j<=n-1;j++)
if(v[j]>v[j+1])
{aux=v[j];
v[j]=v[j+1];
v[j+1]=aux;
}}
cout<<"el numero ordenado es:\n";
for(i=1;i<=n;i++)
{cout<<v[i];
}
if(p==1){
cout<<"\ningrese vector a ordenar:";
cin>>x;
n=n+1;
v[n]=x;}
cout<<"el numero ordenado es:\n";
for(i=1;i<=n;i++)
{cout<<v[i];
}
getch();
}}

                                                  La Ordenación de burbuja 

La Ordenación de burbuja (Bubble Sort en inglés) es un sencillo algoritmo de ordenamiento. Funciona revisando cada elemento de la lista que va a ser ordenada con el siguiente, intercambiándolos de posición si están en el orden equivocado. Es necesario revisar varias veces toda la lista hasta que no se necesiten más intercambios, lo cual significa que la lista está ordenada. Estealgoritmo obtiene su nombre de la forma con la que suben por la lista los elementos durante los intercambios, como si fueran pequeñas "burbujas". También es conocido como el método del intercambio directo.

metodo de seleccion directa con ejemplos en diagrama

Diagrama de flujo de ordenamiento por selección directa

Programación de selección directa en c++

#include<iostream.h>

#include<conio.h>

void main()

{clrscr();

int i,j,a[30], aux,menor,n;

cout<<"ingrese el tamaño del vetor: ";

cin>>n;

for(i=1;i<=n;i++)

{  cout<<"vetor["<<(i)<<"]:";

cin>>a[i];

}

for(i=1;i<n;i++)

{ menor=i;

for(j=i+1;j<=n;j++)

{ if (a[j]<a[menor])

{

menor=j;

}

}

aux =a[i];

a[i]=a[menor];

a[menor]=aux;

}

 cout<<"el orden es:"<<endl;

for(i=1;i<=n;i++)

{

 cout<< a[i];

}

 getch();

3.- SELECCION

El ordenamiento por selección (Selection Sort en inglés) es un algoritmo de ordenamiento que requiere O operaciones para ordenar una lista de n elementos

Su funcionamiento es el siguiente:

• Buscar el mínimo elemento de la lista
• Intercambiarlo con el primero
• Buscar el siguiente mínimo en el resto de la lista
• Intercambiarlo con el segundo

Y en general:

• Buscar el mínimo elemento entre una posición i y el final de la lista
• Intercambiar el mínimo con el elemento de la posición i

EJEMPLO:

 

método de insersion estructura con su ejemplo

Método de Inserción


Método de Inserción Este método también se denomina “método del jugador de cartas”, por la semejanza con la forma de clasificar las cartas de una baraja, insertando cada carta en el lugar adecuado. El algoritmo ordena los dos primeros elementos de la lista, a continuación el tercer elemento se inserta en la posición que corresponda, el cuarto se inserta en la lista de tres elementos, y así sucesivamente. Este proceso continua hasta que la lista este totalmente ordenada. Sea una lista A[1], A[2], ... A[n]. Los pasos a dar para una ordenación ascendente son: 1. Ordenar A[1] y A[2]. 2. Comparar A[3] con A[2], si A[3] es mayor o igual a que A[2], sigue con el siguiente elemento si no se compara A[3] con A[1]; si A[3] es mayor o igual que A[1], insertar A[3] entre A[1] yA[2]. Si A[3] es menor que A[1], entonces transferir A[3] a A[1], A[1] a A[2] y A[2] a A[3]. 3. Se suponen ordenados los n-1 primeros elementos y corresponde insertar el n-ésimo elemento. Si A[m] es mayor que A[k] (con K = 1, 2, ..., m-1), se debe correr una posición A[k+1], ... A[m-1] y almacenar A[m] en la posición k+1.



Consideremos el mismo arreglo del ejemplo anterior { 7, 2, 8, 3, 5, 1 }. El proceso sería de la siguiente manera: 

1ra iteración, i permanece fijo en la casilla 1 y j se decrementa mientras el elemento es menor a j: { 7, 2, 8, 3, 5, 1 } tem = 2, j = 0, mientras j >= 0 y tem < 7, { 7, 7, 8, 3, 5, 1 }, j se decrementa en 1 { 7, 7, 8, 3, 5, 1 } tem = 2, j = -1, mientras j >=0, rompe mientras, tem ingresa { 2, 7, 8, 3, 5, 1 } 

2da iteración, i permanece fijo en la casilla 2 y j se decrementa mientras el elemento es menor a j: { 2, 7, 8, 3, 5, 1 } tem = 8, j = 1, mientras j >= 0 y tem < 7, rompe mientras { 2, 7, 8, 3, 5, 1 } 

3ra iteración, i permanece fijo en la casilla 3 y j se decrementa mientras el elemento es menor a j: { 2, 7, 8, 3, 5, 1 } tem = 3, j = 2, mientras j >= 0 y tem < 8, { 2, 7, 8, 8, 5, 1 }, j se decrementa en 1 { 2, 7, 8, 8, 5, 1 } tem = 3, j = 1, mientras j >= 0 y tem < 7, { 2, 7, 7, 8, 5, 1 }, j se decrementa en 1 { 2, 7, 7, 8, 5, 1 } tem = 3, j = 0, mientras j >= 0 y tem < 2, rompe, tem ingresa { 2, 3, 7, 8, 5, 1 }

 4ta iteración, i permanece fijo en la casilla 4 y j se decrementa mientras el elemento es menor a j: { 2, 3, 7, 8, 5, 1 } tem = 5, j = 3, mientras j >= 0 y tem < 8, { 2, 3, 7, 8, 8, 1 }, j se decrementa en 1 { 2, 3, 7, 8, 8, 1 } tem = 5, j = 2, mientras j >= 0 y tem < 7, { 2, 3, 7, 7, 8, 1 }, j se decrementa en 1 { 2, 3, 7, 7, 8, 1 } tem = 5, j = 1, mientras j >= 0 y tem < 3, rompe, tem ingresa { 2, 3, 5, 7, 8, 1 }

 5ta iteración, i permanece fijo en la casilla 5 y j se decrementa mientras el elemento es menor a j: { 2, 3, 5, 7, 8, 1 } tem = 1, j = 4, mientras j >= 0 y tem < 8, { 2, 3, 5, 7, 8, 8 }, j se decrementa en 1 { 2, 3, 5, 7, 8, 8 } tem = 1, j = 3, mientras j >= 0 y tem < 7, { 2, 3, 5, 7, 7, 8 }, j se decrementa en 1

{ 2, 3, 5, 7, 7, 8 } tem = 1, j = 2, mientras j >= 0 y tem < 5, { 2, 3, 5, 5, 7, 8 }, j se decrementa en 1
 { 2, 3, 5, 5, 7, 8 } tem = 1, j = 1, mientras j >= 0 y tem < 3, { 2, 3, 3, 5, 7, 8 }, j se decrementa en 1 
{ 2, 3, 3, 5, 7, 8 } tem = 1, j = 0, mientras j >= 0 y tem < 2, { 2, 2, 3, 5, 7, 8 }, j se decrementa en 1
 { 2, 2, 3, 5, 7, 8 } tem = 1, j = -1, mientras j >= 0, rompe mientras, tem ingresa { 1, 2, 3, 5, 7, 8 }   

 Diagrama de flujo de ordenamiento por inserción

diagrama de flujo : el area de un triangulo por for

METODO BURBUJA

ORDENAMIENTO POR SELECCIÓN

ORDENAMIENTO POR SELECCION  
El ordenamiento por selección (Selection Sort en inglés) es un algoritmo de ordenamiento que requiere O operaciones para ordenar una lista de n elementos.
Su funcionamiento es el siguiente:

• Buscar el mínimo elemento de la lista
• Intercambiarlo con el primero
• Buscar el mínimo en el resto de la lista
• Intercambiarlo con el segundo

Y en general:

• Buscar el mínimo elemento entre una posición i y el final de la lista
• Intercambiar el mínimo con el elemento de la posición i

De esta manera se puede escribir el siguiente pseudocódigo para ordenar una lista de n elementos indexados desde el 1:

para i=1 hasta n-1
    minimo = i;
    para j=i+1 hasta n
        si lista[j] < lista[minimo] entonces
            minimo = j /* (!) */
        fin si
    fin para
    intercambiar(lista[i], lista[minimo])
fin para 

 
seleccion 
#include<stdio.h> 
#include<conio.h> 
int x[4]={1,4,8,6}; 
int n=4,j=0,i=0; 
int temp=0,minimo=0; 
void main(){ 
clrscr(); 
for(i=0;i<n-1;i++) 
{ 
minimo=i; 
for(j=i+1;j<n;j++) 
{ 
if(x[minimo] > x[j]) 
{ 
minimo=j; 
} 
} 
temp=x[minimo]; 
x[minimo]=x;
x=temp;
}
for(i=0;i<n;i++)
{
printf("%d",x);
}
getch();
}EJERCICIOS METODO DE ORDENAMIENTO EJERCICIO 01

#include <stdio.h>
#define SIZE 7
void main(void) {
  int vector[SIZE];
  int j, i, temp;
  printf("Introduce los %d valores para ordenar:\n", SIZE);
  for(i=0; i<SIZE; i++) {
     printf("%d: ", i+1);
     scanf("%d", &vector[i]);
     printf("\n");
  }
  /* se aplica el algoritmo de la burbuja */
  for(i=0; i<(SIZE-1); i++) {
     for (j=i+1; j<SIZE; j++) {
        if(vector[j]<vector[i]) {
            temp=vector[j];
            vector[j]=vector[i];
            vector[i]=temp;
        }
     }
  }
  printf("El vector ordenado es:\n");
  for(i=0; i<SIZE ; i++) {
     printf("%d ", vector[i]);
  }
  printf("\n");
}

EJERCIO 02

#include <stdio.h>

#include <stdlib.h>

#include <string.h>
 

void OrdenaBurbuja (float v[], int n)

{

int t, h, e;

for (h=1; h<n; h++)

{

for(e=0; e<n;e++)

{

if (v[e]>v[e+1])

{

v[e+1] = t;

v[e] = v[e+1];

t= v[e];

}

}

}

}
 
 

void ImprimirVector(float v[], int n)

{

int i; 

for (i=0; i<n; i++)

{

printf("%f ", v[i]);

}

}
 

int main(int argc, char *argv[])

{

if(strcmp(argv[1], "burbuja")==0)

{

int n, i, m=2, o;

float *v;

{

n=argc-2; 

v =(float *)malloc(n*sizeof(float));

for (i=0; i<n; i++)

{

v[i] = atof(argv[i+2]);

}

}

OrdenaBurbuja(v, n);

ImprimirVector(v, n);

}

system("PAUSE"); 

return 0;

}

ORDENAMIENTO POR INSERCIÓN

ORDENAMIENTO POR INSERCION  
El ordenamiento por inserción (insertion sort en inglés) es una manera muy natural de ordenar para un ser humano, y puede usarse fácilmente para ordenar un mazo de cartas numeradas en forma arbitraria. Requiere O(n²) operaciones para ordenar una lista de n elementos.

Inicialmente se tiene un solo elemento, que obviamente es un conjunto ordenado. Después, cuando hay k elementos ordenados de menor a mayor, se toma el elemento k+1 y se compara con todos los elementos ya ordenados, deteniéndose cuando se encuentra un elemento menor (todos los elementos mayores han sido desplazados una posición a la derecha) o cuando ya no se encuentran elementos (todos los elementos fueron desplazados y este es el más pequeño). En este punto se inserta el elemento k+1 debiendo desplazarse los demás elementos.

iinserccion
#include<stdio.h>
#include<conio.h>
int a[4]={4,1,7,2};
int n=4;
int i,j,aux;
void main(){
clrscr();
for(i=1;i<n;i++)
{
j=i;
aux=a;
while(j>0 && aux<a[j-1])
{
a[j]=a[j-1];
j--;
}
a[j]=aux;
}
for(i=0;i<4;i++)
{
printf("%d",a);
}
getch();
} 

ORDENAMIENTO SHELL

ORDENAMIENTO SHELL El ordenamiento Shell (Shell sort en inglés) es un algoritmo de ordenamiento. El método se denomina Shell en honor de su inventor Donald Shell. Su implementación original, requiere O(n²) comparaciones e intercambios en el peor caso. Un cambio menor presentado en el libro de V. Pratt produce una implementación con un rendimiento de O(n log² n) en el peor caso. Esto es mejor que las O(n²) comparaciones requeridas por algoritmos simples pero peor que el óptimo O(n log n). Aunque es fácil desarrollar un sentido intuitivo de cómo funciona este algoritmo, es muy difícil analizar su tiempo de ejecución. El algoritmo Shell sort mejora el ordenamiento por inserción comparando elementos separados por un espacio de varias posiciones. Esto permite que un elemento haga "pasos más grandes" hacia su posición esperada. Los pasos múltiples sobre los datos se hacen con tamaños de espacio cada vez más pequeños. El último paso del Shell sort es un simple ordenamiento por inserción, pero para entonces, ya está garantizado que los datos del vector están casi ordenados.  

shell
#include<stdio.h>
#include<conio.h>
int a[5];
int n=5;
void main()
{
int inter=(n/2),i=0,j=0,k=0,aux;
clrscr();
for (i=0; i<5; i++)
{
printf("INSERTA UN VALOR DEL INDICE %d", i);
scanf("%d",& a);
}
while(inter>0){
for(i=inter;i<n;i++)
{
j=i-inter;
while(j>=0) {
k=j+inter;
if(a[j]<=a[k]){
j--;
}
else{
aux=a[j];
a[j]=a[k];
a[k]=aux;
j=j-inter;
}
}
}
inter=inter/2;
}
for(i=0;i<5;i++)
{
printf("%d n",a);
getch();
}
}   

ORDENAMIENTO DE BURBUJA

ORDENAMIENTO DE BURBUJA

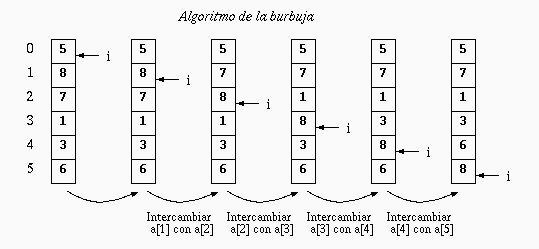
La Ordenación de burbuja (Bubble Sort en inglés) es un sencillo algoritmo de ordenamiento. Funciona revisando cada elemento de la lista que va a ser ordenada con el siguiente, intercambiándolos de posición si están en el orden equivocado. Es necesario revisar varias veces toda la lista hasta que no se necesiten más intercambios, lo cual significa que la lista está ordenada. Este algoritmo obtiene su nombre de la forma con la que suben por la lista los elementos durante los intercambios, como si fueran pequeñas "burbujas". También es conocido como el método del intercambio directo. Dado que solo usa comparaciones para operar elementos, se lo considera un algoritmo de comparación, siendo el más sencillo de implementar.
burbuja
#include<stdio.h>
#include<conio.h>
int a[3]={3,2,1};
int i,j,aux,n=3;
void main(){
clrscr();
for(i=0;i<=n;i++){
for(j=0;j<n-1;j++){
if(a[j]>a[j+1]){
aux=a[j];
a[j]=a[j+1];
a[j+1]=aux;
}
}
}
for(i=0;i<3;i++)
{
printf("%d",a);
}
getch(); 

que es el método de ordenamiento

METODOS DE ORDENAMIENTO 
Debido a que las estructuras de datos son utilizadas para almacenar información, para poder recuperar esa información de manera eficiente es deseable que aquella esté ordenada. Existen varios métodos para ordenar las diferentes estructuras de datos básicas.

Añadir leyenda

En general los métodos de ordenamiento no son utilizados con frecuencia, en algunos casos sólo una vez. Hay métodos muy simples de implementar que son útiles en los casos en dónde el número de elementos a ordenar no es muy grande (ej, menos de 500 elementos). Por otro lado hay métodos sofisticados, más difíciles de implementar pero que son más eficientes en cuestión de tiempo de ejecución.

Los métodos sencillos por lo general requieren de aproximadamente n x n pasos para ordenar n elementos.

Los métodos simples son: insertion sort (o por inserción directa) selection sort, bubble sort, y shellsort, en dónde el último es una extensón al insertion sort, siendo más rápido. Los métodos más complejos son el quick-sort, el heap sort, radix y address-calculation sort. El ordenar un grupo de datos significa mover los datos o sus referencias para que queden en una secuencia tal que represente un orden, el cual puede ser numérico, alfabético o incluso alfanumérico, ascendente o descendente.

Se ha dicho que el ordenamiento puede efectuarse moviendo los registros con las claves. El mover un registo completo implica un costo, el cual se incrementa conforme sea mayor el tamaño del registro. Es por ello que es deseable evitar al máximo el movimiento de los registros. Una alternativa es el crear una tabla de referencias a los registros y mover las referencias y no los datos. A continuación se mostrarán los métodos de ordenamiento empezando por el más sencillo y avanzando hacia los mas sofisticados 
La eficiencia de los algoritmos se mide por el número de comparaciones e intercambios que tienen que hacer, es decir, se toma n como el número de elementos que tiene el arreglo a ordenar y se dice que un algoritmo realiza O(n2) comparaciones cuando compara n veces los n elementos, n x n = n2. 

 

que es el método de insersion

Ordenamiento por Inserción

Ordenamiento por Inserción

Ordenamiento por Inserción: Supóngase que se desea ordenar los siguientes claves del arreglo (A) utilizando el método de inserción directa el cual consiste en insertar un elemento del arreglo en la parte izquierda del mismo que ya se encuentra ordenada. Este proceso se repite desde el segundo hasta el n-esimo elemento.

Insercion(A,N)Insercion (A,N), Algoritmo

El algoritmo ordena los elementos del arreglo utlizando el método de inserción directa A es un arreglo de N elementos 
donde I, aux y k son variables de tipo entero

1.- Repetir con I desde 2 hasta N Hacer aux<- A[I] y k<- I-1
a. Repetir mientras(aux < [k]) y (k > 1) , Hacer A[k+1]<- A[k] y k<-- k-1
b. {fin del ciclo del paso 1.1}
c. Si a[k]<=aux Entonces: Hacer A[k+1]<-aux
Si no Hacer A[k+1]<- A[k], A[k]<-A[k]
d. { fin del condicional del paso 1.3}
2. {fin del condicional del paso1}

Implementación

A continuación se muestra el ordenamiento por inserción en distintos lenguajes de programación:

C

void Insercion(int numbers[], int array_size) {
  int i, a, index;
  for (i=1; i < array_size; i++) {
    index = numbers[i];
    a = i-1;
    while (a >= 0 && numbers[a] > index) {
      numbers[a + 1] = numbers[a];
      a--;
    }
    numbers[a+1] = index;
  }
}

Python

def Insercion(numeros): #numeros es una lista
  tama = len(numeros) #tamaño de la lista
  i=0
  for i in range(tama):
    indice = numeros[i]
    a = i-1
    while (a >= 0 and numeros[a] > indice):
      numeros[a+1] = numeros[a]
      a = a-1
    numeros[a+1] = indice
  print numeros #imprime la lista ordenada

PHP

function Insercion($arr){
  $count = count($arr);
  for($i=1; $i<$count; $i++){
    $tmp = $arr[$i];
    for ($j=$i-1; $j>=0 && $arr[$j] > $tmp; $j--)
      $arr[$j+1] = $arr[$j];
      $arr[$j] = $tmp;
  }
  return $arr;
}

Prueba de escritorio

Si A= 15, 67, 08, 16, 44, 27, 12, 35
1ª pasada 08, 67, 15, 16, 44, 27, 12, 35
2ª pasada 08, 15, 67, 16, 44, 27, 12, 35
3ª pasada 08, 15, 16, 67, 44, 27, 12, 35
4ª pasada 08, 15, 16, 44, 67, 27, 12, 35
5ª pasada 08, 15, 16, 44, 27, 67, 12, 35
6ª pasada 08, 15, 16, 44, 27, 12, 67, 35
7ª pasada 08, 15, 16, 44, 27, 12, 35, 67

Análisis de la eficiencia 

En general afirmar que si el arreglo se encuentra ordenado se efectúan como máximo n-1 comparaciones y o movimientos entre elementos Cmin = n-1.

El número máximo de comparaciones y movimientos se produce cuando los elementos del arreglo están en orden inverso
Cmax = 1+2+3+............+(n-1) = n*(n-1)/2
Cmax= (n2-n)/2

El número de comparaciones promedio que es cuando los elementos aparecen en el arreglo en forma aleatoria, puede ser calculado mediante la suma de las comparaciones mínimas y máximas divididas entre 2.
Cmed = [(n-1) + (n2-n)/2]/2
Al hacer la operación, nos queda:
Cmed = (n2+n-2)/4
Respecto al número de movimientos Knuth obtiene los siguiente:
Mmin = 0
Mmed = (n2-n)/4
Mmax = (n2-n)/2

Tiempo de ejecución 

El tiempo necesario para ejecutar el algoritmo es proporcionar a n2, O(n2).
A pesar de ser un método ineficiente y recomendable solo cuando n es pequeña, el método de inserción directa se comporta mejor que el método de intercambio directo.

•